To solve the Petersen Graph Zome Challenge, I wrote a computer program that methodically enumerates all Zome constructions that are topologically equivalent to the Petersen Graph. Any solutions are printed out. This page decribes the approach taken to acheive these goals.
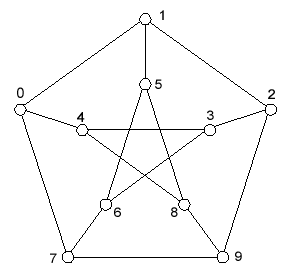
Consider the Petersen Graph shown here...

This graph can be considered as three cycles of length five plus three extra segments. For example...
| Cycle 0: | 0 | 1 | 2 | 3 | 4 |
| Cycle 1: | 0 | 1 | 5 | 6 | 7 |
| Cycle 2 | 7 | 0 | 4 | 8 | 9 |
| Line 0: | 2 | 9 | |||
| Line 1: | 3 | 6 | |||
| Line 2: | 5 | 8 |
One way to enumerate all Petersen Graph constructions is to:
Having written such a program, I can report that a non-self-intersecting equilateral Petersen Graph is not Zome constructible. I then relaxed the checks in step 3 to accept cycles even if point 9 was not a neighbor of point 2 (but the program still considered segment 2-to-9 when counting intersections).
For each Petersen Graph found, the program prints the three cycles using the nomenclature described in Analytic Zome, the number of intersections, and the length of the 2-to-9 segment (based on the other 14 segments having length 1). Relaxing the restriction on the length of the 15th strut allows for many non-intersecting Petersen graphs that are mostly Zome construcible (the length of the 15th strut is often not a Zome length) and even some that are completely Zome constructible (the length of the 15th strut is a Zome length). The different lengths of the 15th strut are shown in the table below along with a equivalent expressions. Can you determine expressions for s? t? u? v? w? x? y? z? If so, please email them to zome@smartsc.com.
Many of these lengths do not correspond to Zome strut lengths and are therefore not Zome constructible. I have only constructed one whose 15th strut had a length of 1.61803 (T). Others that are probably Zome constructible using blue struts have a 15th strut length of 0.61803 (1/T), 2.0, and 3.23607 (2T), although the latter two would involve an extra node. Others might be constructible using two yellow or red struts as the 15th strut, but they would also use an extra node.
The program's output was used to generate the lists of non-intersecting Petersen Graphs that can be viewed as virtual Zome constructions on the Virtual Zome Petersen Graphs page. Note that you must have a VRML plug-in for your browser. I have had much better luck viewing VRML in Netscape than in Internet Explorer.
| Length of 15th Strut |
Equivalent expression |
| 0.61803 | 1/T |
| 0.72654 | sqrt(2+T)/(T+1) |
| 0.87403 | sqrt(2)/T |
| 1.07047 | sqrt(3)/T |
| 1.17557 | srt(2+T)/T |
| 1.41421 | sqrt(2) |
| 1.54336 | z? |
| 1.61803 | T |
| 1.66251 | y? |
| 1.73205 | sqrt(3) |
| 1.77367 | x? |
| 1.83901 | w? |
| 1.90211 | sqrt(2+T) |
| 2.0 | 2 |
| 2.09331 | v? |
| 2.14896 | u? |
| 2.28825 | T*sqrt(2) |
| 2.37024 | t? |
| 2.57255 | s? |
| 2.68999 | T*y? |
| 2.80252 | T*sqrt(3) |
| 2.97558 | T*w? |
| 3.23607 | 2*T |