First, a few definitions:

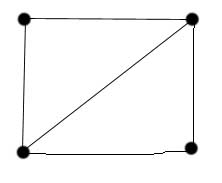
graph: any set of vertices and lines connecting them

planar: a property of a graph; in a planar graph, no lines cross

degree: the degree of a vertex is the number of lines attached to it

diameter: The maximum number of the minimum number of steps required to get from any point in the graph to any other point in the graph

Some examples:

This graph has a diameter of 2, is planar, has a minimum degree of 2, and a maximum degree of 3. Adding the square's other diagonal would change the diameter to 1, would make the graph no longer planar, and would give it a minimum degree of 3.

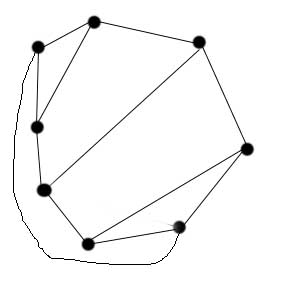
This graph has 8 vertices, has a constant degree of 3, is planar, and has a diameter of 3. Making the only non-straight line cut straight across the graph would make the graph non-planar, but nothing else would change.

The actual problem has three parts.

(1) Construct a graph with 12 vertices that has a constant degree of 3, is planar, and has a diameter of exactly 3.

(2) Construct a graph with more than 12 vertices that has a constant degree of 3, is planar, and has a diameter of exactly 3.

(3) Show that it's impossible to create a graph with the properties in (1) and (2) with an odd number of vertices.

For the record, parts (1) and (3) are relatively easy. Part 2 is very difficult.
Back...