Scientific sports research has traditionally been limited primarily to baseball (Cover, 1977; Freeze, 1974; Lindsey, 1959; Lindsey, 1963, Pankin, 1978). Popular work by Bill James and others (James, 1984, 1985, 1986, 1987, 1988; Thorn & Palmer, 1985; Thorn, Palmer, and Routher, 1991), though oftentimes not mathematically rigorous, has provided great insights into America's pastime. Research on organized basketball, on the other hand, has been very limited (Albright, 1978). Recent attempts at popular, non-rigorous basketball research (Heeren, 1988, 1990; Manley, 1987, 1988, 1989; Trupin & Couzens, 1989) have not had near the effects that similar baseball research has had. This may be because the statistical base, which is so large in baseball, has not been built up in basketball. One of the goals of this paper is to help build this statistical base by introducing a new scoring method for basketball games that identifies new and valuable statistics for teams and, eventually, players.
The second goal of this paper is to check the accuracy of a binomial distribution in describing the game of basketball. A simple way to check this is to test a relationship known as the Pythagorean Method. The Pythagorean Method is a simple mathematical relationship between the number of points scored and allowed by a team and the team's winning percentage. First used by James (1984) in baseball work, we will empirically expand the Pythagorean Method to basketball and compare results with those predicted by a simple binomial model of the game.
The new scoring system we developed is not designed to replace traditional scoring methods, which are quick and efficient for tabulating cumulative statistics. This scoring system, known as the Possession Scoring System, was designed to collect as much information as possible about the game, which means giving up the simple tabulating techniques. All that is really needed to score a game using this system is something to write with, four sheets of lined paper (both sides will likely be used), and a decent understanding of basketball scoring rules. The NBA usually has several people working to keep official stats, but this method only requires one person. That one person, however, must work fast.
The System is very simple. It focuses on the player with the ball, following the ball from player to player until the ball is turned over to the opposition through a shot attempt or turnover. For example, a scoresheet for part of a Detroit-Los Angeles Lakers game might look something like this: [Editor's Note: In the original document, many of the following symbols were in subscripts or superscripts.]
23 LA 32D 4 42 4 32 ++B 22 D 11D 4D 53 ++L 24 LA 45D 32D 42 F10(2) xo 25 D 4D 40 11D +Y3pt 24 LA 32D 42D 4 21 -X 27 D 10R 4D 23 ++R FB 27 LA 32 45D 32D 45 32D -2 32R +L F40(1) o TIME 1:13 27 D 11D 53 11 15 TRVL TO 27 LA 32D 4D 42D -R BK22 27 D 11RD BP TO 29 LA 4STL D 32D 4++R FB 29 D 11D 4D 40 -A 11R +3 29 LA 32 -Y END 1Q
This brief section of a hypothetical scoresheet shows the end of the first quarter between Detroit and Los Angeles. The opening page of the scoresheet would note certain information about the teams, such as which is the home team, their starting lineups, who is favored, the game time, and any other relevant information. For instance, if it was Game 6 of the NBA Championship Series, it would be noted.
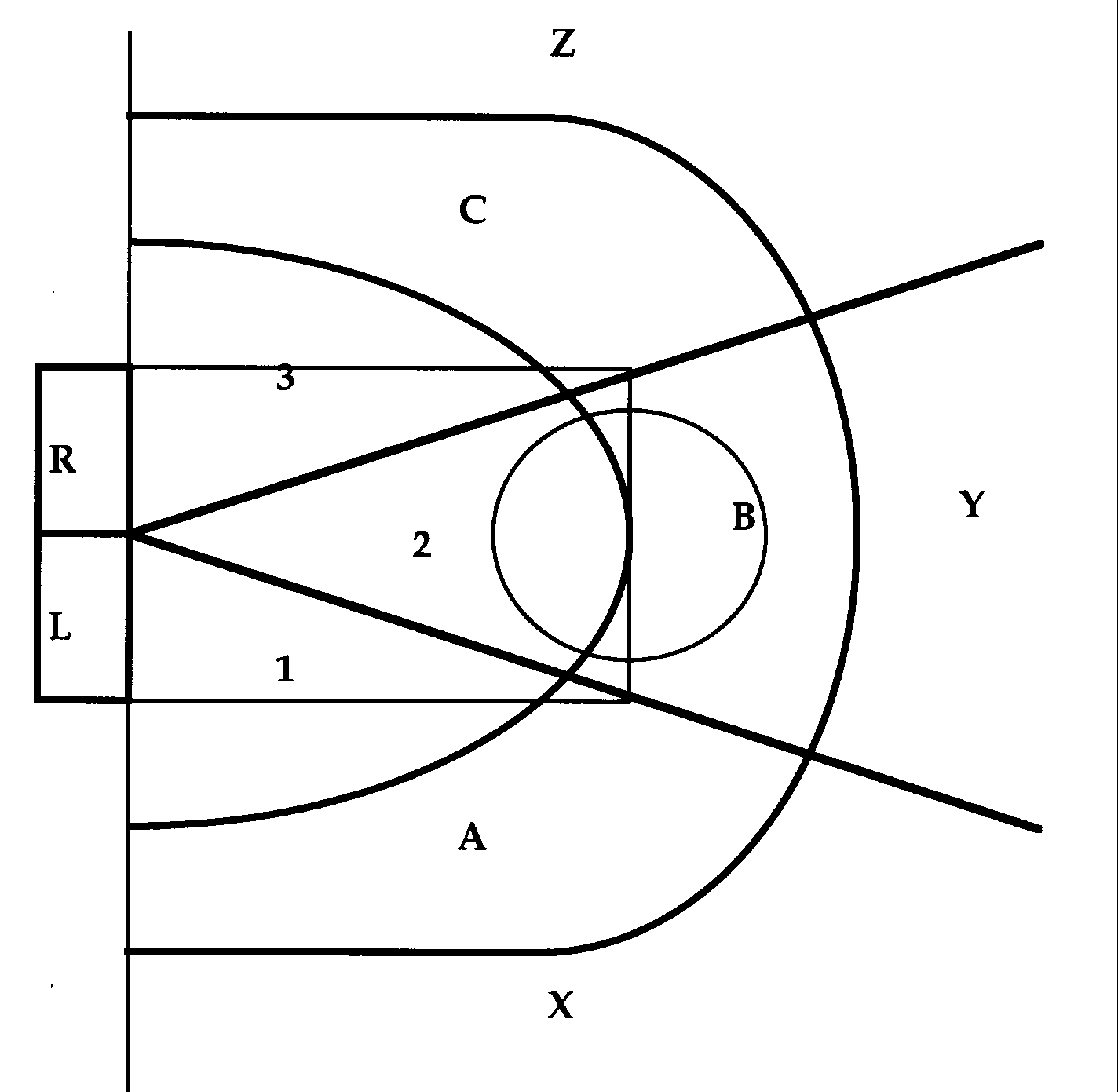
On the left is the running score of the game. On the first line, the number 23 appears to the left of 'LA', meaning that the Lakers ended the possession with 23 points. The numbers to the right of 'LA' or 'D' on each line correspond to the jersey numbers of the players as they touch the ball. For example, the first line shows that the Lakers' number 32, Magic Johnson, dribbled (32D), then passed to Byron Scott (number 4), who passed to James Worthy (number 42), who passed back to Scott (4), back to Johnson (32) who made a jump shot on the assist from Scott (4 32 ++B). [The complete Laker possession: 32D 4 42 4 32 ++B] A flat line (-) next to a number indicates that the person with that number shot the ball. If the flat line is crossed vertically (+), then the shot went in. If a second vertical line is present (++), then an assist - officially defined as a pass that "directly leads to a basket" - is credited to the player whose number is listed previous to the one who made the shot. The subscript next to the symbol indicating a shot is a shorthand for where the shot was attempted on the court. In this case, the subscript B means that Johnson took the shot from between the free throw line and the three point line in the middle of the court. All the regions of the court are seen in Figure 1.

On the second line, Detroit has the ball. Isiah Thomas dribbles (11D) up the court, then passes it to Joe Dumars (4). Dumars dribbles (4D) then finds James Edwards for a layup from the left side (53 ++L) for the Pistons' 21st and 22nd points. [The Detroit possession: 11D 4D 53 ++L]
Next, Los Angeles has the ball again. A.C. Green (45) this time dribbles the ball up (45D), gives it to Johnson who then maneuvers for a pass into Worthy. Worthy is fouled by Dennis Rodman, his second (F10(2)), which sends Worthy to the line for two free throws. He misses the first (x) and makes the second (o), giving the Lakers a 24-22 lead over the Pistons. [Laker possession: 45D 32D 42 F10(2) xo]
Then it's Detroit's turn. Dumars dribbles up, passes to Bill Laimbeer (40), who then gives it up to Thomas. Thomas dribbles around, then takes and makes a three point shot from straight-away (11 +Y3pt). No assist was credited, so there is only one vertical line. Detroit leads 25-24. [Detroit possession: 4D 40 11D +Y3pt]
Johnson brings the ball up for the Lakers next possession and passes to Worthy. He dribbles, then finds Scott, who swings it to Michael Cooper (21). Cooper misses his three point attempt from the left side (21 -X). [Laker possession: 32D 42D 4 21 -X]
The missed shot is rebounded by Rodman (10R), who outlets to Dumars streaking up the court. Dumars hits Mark Aguirre on the right for a fast-break (FB) layup (4D 23 ++R FB). [Detroit possession: 10R 4D 23 ++R FB]
The Lakers get the ball, down 27-24. Johnson hands the ball to Green to bring up the court. When Green reaches the front court, he finds Johnson and Johnson dribbles around. He gets the ball back to Green so that he can get himself free. Green gives it back to Johnson, who drives to the basket and misses a shot from the middle of the lane (32D -2). Johnson gets his own rebound (32R), puts it back up and in with a foul on Laimbeer to help complete a three point play (32R +L F40(1) o ). This ties the score at 27 and time is called (TIME 1:13). [Laker possession: 32 45D 32D 45 32D -2 32R +L F40(1) TIME 1:13]
Detroit's Thomas has the ball when play resumes. He dribbles up, passes to Edwards, who passes it back to Thomas, who finds Vinnie Johnson. Johnson travels and turns the ball over (15 TRVL TO). The ball goes back to the Lakers with the score still tied at 27. [Detroit possession: 11D 53 11 15 TRVL TO]
The Lakers' Johnson brings it up, finds Scott, who then dribbles trying to free himself and/or pull the defense off Worthy. Worthy gets the ball from Scott and puts it on the floor going for the layup, but John Salley is there to block it away (42D -R BK22). A wasted possession for the Lakers. [Laker possession: 32D 4D 42D -R BK22]
The ball goes back to Detroit via a Thomas rebound, who starts dribbling up court looking for another break (11RD). He tries to sneak a pass past Byron Scott, but instead turns it over on the bad pass (BP TO). [Detroit possession: 11RD BP TO]
After Scott's steal (4STL ), he dribbles up looking for a Laker break. He finds Johnson, who then returns the favor by assisting on a Scott layup (or dunk). The Lakers go ahead 29-27. [Laker possession: 4STL D 32D 4++R FB]
Detroit comes back looking for the last shot. Thomas dribbles up and passes to Dumars. Dumars sees the clock running down and drives, kicking it out to Laimbeer for a jumper from the left side. It misses, but Thomas is in the right place at the right time for the rebound. He throws up a high arcing shot from just outside the right side of the key and it falls. Tied at 29. [Detroit possession: 11D 4D 40 -A 11R +3]
Magic Johnson throws up a length-of-the-court shot to end the first quarter. The score remains 29-all. [Laker final possession: 32 -Y]
In this scoresheet, we tried to demonstrate most of the common situations in basketball. Some other common situations and how they are denoted: Jump balls are simply noted by the word 'Jump' and the numbers of the two players involved. Rebounds that go out of bounds are denoted by ROB. Sometimes it is necessary to note who is inbounding the ball; for instance, if number 22 inbounds the ball and commits a turnover on a bad pass: OB22 BP TO.
Recording all this information during a fast-paced basketball game is not easy, but it becomes fairly routine after practicing a few times. Often during the heat of a game, it is easy to forget to note things like fast breaks or blocked shots, but the fundamental structure of the system - noting who touches the ball and whether they shoot it or pass it - is not difficult to maintain.
An important thing to notice in this demonstration is how teams alternate possession during a game. In this example, the Lakers would score, commit a turnover, or not get a rebound, then Detroit would get the ball. For each opportunity that the Lakers get to score, the Pistons also get a chance. By getting an offensive rebound, a team is seen as 'keeping its opportunity to score alive' rather than 'creating another opportunity'. By scoring this way, possessions are equal for both teams in a game. Just as each team has the same 48 minutes in a game to outscore its opponent, each team also has the same 100 or so possessions in a game with which to outscore its opponent. [Note: This is the same way Albright (1978) defined possessions, but not how Manley (1988) defines them.]
One result of using this scoring method is that we can calculate probabilities of scoring for both teams over an equal number of trials. [Note: In a non-overtime game, it is possible that one team will have as many as two more possessions than its opponents. It appears unlikely, however, that any one team will consistently have more or fewer possessions than its opponents over the course of an 82 game season.] A scoring possession is defined as a possession on which one or more points are scored. A floor percentage (floor%) is then defined as the ratio of scoring possessions to total possessions. Over the course of a season, we can estimate the offensive floor%, ps, and the defensive floor%, pds, through the following method.
First of all, we assume that scoring possessions are worth 2 points each, meaning that total points are equal to twice the number of scoring possessions. This is obviously an approximation, but it is not a bad one for professional basketball (the National Basketball Association, or NBA), where teams most often score 2 points per scoring possession. The number of 3 point possessions is fairly closely balanced by the number of 1 point possessions, though this depends somewhat on the team in question. By assuming 2 points per scoring possession, we estimate the values of ps and pds by calculating points per possession and dividing by 2:
ps = scoring possessions/total possessions = (points/2)/total possessions 1
pds = scoring possessions allowed/total possessions
= (points allowed/2)/(total possessions) 2
[Note: There is another, more theoretical, and more complicated way to estimate ps, but it will not be used here because the same method cannot currently be used to find pds and because the method is complex enough to be another paper in itself.] In equations 1 and 2, there are only three things that need to be known: points, points allowed, and total possessions. The number of points scored and allowed by a team over the course of the season are official stats that need not be estimated. Total possessions, however, must be estimated from the following formula, which was determined by comparing personal scoresheets of games with official statistics:
Total possessions = 0.5*[(FGA - OR + TO + 0.4 * FTA)off +
(FGA - OR + TO + 0.4 * FTA)def] 3
where FGA is the number of field goals attempted, OR is the number of offensive rebounds, TO is the number of turnovers, FTA is the number of free throws attempted, and the subscripts 'off' and 'def' correspond to offensive and defensive statistics, respectively. The values in the parentheses are estimates of offensive and defensive possessions and we are just taking the average of the two. Note that this formula works by counting the ways that a possession can end: a missed field goal attempt that is not rebounded by the offense (FGA - OR), a turnover, and a certain fraction of free throw attempts.
The accuracy of equation 3 has not been seriously tested, but it appears to be fairly good. For example, we can get a rough check by examining the final stats from the Laker-Detroit scoresheet above:
Sc.
FG FGA FG% FT FTA FT% OR DR TR AST TO PTS Poss Poss.
D 4 5 80 0 0 --- 1 2 3 2 2 9 4 6
LA 3 7 43 2 3 67 1 0 1 2 0 8 4 7
The formula estimates 6.6 possessions for each team, which is between the 6 possessions Detroit had and the 7 LA had. [Note: Equation 3 actually calculates 6.0 possessions for Detroit and 7.2 possessions for LA. Averaging the two estimates is assumed to be better when larger statistical samples are available and errors - due to team rebounds and differences from 0.4 * FTA - become larger.] At the end of the season, the offensive and defensive estimates of possessions for individual teams are usually within 1% of each other, indicating that the equation is consistent over larger data samples.
We can now estimate offensive and defensive floor%'s, ps and pds, for the 27 NBA teams from the 1990-91 season. These are seen in Table I.
Points Points Est'd Est'd Est'd Team Scored Allowed Poss. ps pds Atlanta 9003 8940 8247 .546 .542 Boston 9145 8668 8286 .552 .523 Charlotte 8428 8858 8164 .516 .543 Chicago 9024 8278 8018 .563 .516 Cleveland 8343 8545 8005 .521 .534 Dallas 8195 8570 7890 .519 .543 Denver 9828 10723 9530 .516 .563 Detroit 8205 7937 7736 .530 .513 Golden St. 9564 9430 8703 .549 .542 Houston 8753 8466 8309 .527 .509 Indiana 9159 9191 8338 .549 .551 LA Clippers 8491 8774 8390 .506 .523 LA Lakers 8717 8164 7963 .547 .513 Miami 8349 8840 8344 .500 .530 Milwaukee 8727 8524 8105 .538 .526 Minnesota 8169 8491 7853 .520 .541 New Jersey 8441 8811 8375 .504 .526 New York 8455 8474 8025 .527 .528 Orlando 8684 9010 8363 .519 .539 Philadelphia 8641 8656 8144 .531 .531 Phoenix 9348 8811 8462 .552 .521 Portland 9407 8695 8510 .553 .511 Sacramento 7928 8484 7907 .501 .536 San Antonio 8782 8412 8294 .529 .507 Seattle 8744 8643 8128 .538 .532 Utah 8527 8254 7982 .534 .517 Washington 8313 8721 8242 .504 .529
Estimating Winning Percentage From ps and pds
In order to estimate a winning percentage from ps and pds, we assume that basketball possessions are Bernoulli trials. Over the course of a season, the number of scores a team has and allows in a game is assumed to vary as a binomial with percentages ps and pds, respectively, and with the number of trials being equal to the number of possessions a team averages in a game.
By strict definition, basketball possessions are obviously not Bernoulli trials. First of all, each possession can result in 0, 1, 2, 3, or more points, not 'success' or 'failure' as specified for Bernoulli trials in a binomial distribution. [Note: We have taken 'success' to mean scoring 1 or more points on a possession and 'failure' to mean 0 points.] A second problem with calling possessions Bernoulli trials is that the probability of scoring is not constant from possession to possession. A team does not play its best players all the time, rotating in new players as the better ones get tired. These substitutes often will not score as often as the starters, i.e. they will not have the same probability of success as the starters. Even among a team of 5 players trying to score, there is non-random variability. Hot streaks, cold streaks, and conscious attempts to get the ball to certain players at certain times will change the probability of success in certain segments of a game. In short, the process of a basketball team moving the ball, shooting, and rebounding is a much more complicated process than a simple Bernoulli trial.
Nevertheless, we will use a binomial distribution to describe offensive and defensive point distribution and show that it does give reasonable predictions of winning percentages. First of all, the probability that the offense wins, given an offensive floor% of ps and a defensive floor% of pds, is given by
P[win] = Sum[P[X=i;B(N,p_ds)]*(P[Y>i;B(N, p_s)]+alpha*P[Y=i;B(N,p_s)]), i=0,N] 4
where X and Y are random variables from binomial distributions with means Npds and Nps (representing the number of defensive and offensive scores in a game), respectively, where N is the average number of possessions for each team in a game, and a is the percentage of times this team wins when it goes to overtime. Because overtime is essentially a mini-game with roughly 1/10th as many possessions as in a complete 48 minute game, regardless of how good or bad a team is, it is likely to be more of an average team in overtime games. This means that a is close to 0.500, which is the value we have nominally set it to. A quick example shows this not to be a bad assumption. For N = 100, ps = 0.55, and pds = 0.53, the value of the equation 4 is 0.612, meaning that a team that scores on 55% of its 100 possessions per game and allows its opponents to score on 53% of their possessions will win approximately 61.2% of their games. Adjusting a to 0.618 brings the value of equation 4 also to 0.618, which is not greatly different. At the extremes, if a = 1, then P[win] = 0.639, or if a = 0, then P[win] = 0.584. An especially good or bad overtime team can mean a difference of roughly ±0.025, or two games over the course of a season. In fact, the theoretical value of a can be determined from an infinite number of imbedded sums in the form of equation 4, where the upper limit on the sum becomes the number of possessions in each overtime. In short, a depends on the values of ps, pds, and N, and is about 0.54 for these example values, making P[win] approximately 0.614.
Because N is large in basketball, commonly ~100+, we have replaced equation 4 in computations with the simpler normal approximation:
P[win] _ P{Z<Z*=(p_s-p_ds)/sqrt[(p_s*(1-p_s)+p_ds*(1-p_ds))/N]} 5
Using the above example values for ps, pds, and N, this expression yields a winning percentage of 0.612. [Note: It would be necessary to define a binomial distribution for fractions of possessions (trials) if we do not round possessions/game to the nearest integer in equation 4.]
Equation 5 was applied to all 27 of the NBA teams for the 1990-91 season and the results are seen in the 'Binomial P[Z < Z*]' column of Table II, where Z* comes from equation 5:
Z*=(p_s-p_ds)/sqrt[(p_s*(1-p_s)+p_ds*(1-p_ds))/N]
Actual winning percentages for all of the teams are shown in the far right column of the table. A complete examination of the two columns reveals that the binomial predictions are generally closer to 0.500 than they should be, implying that the binomial standard deviation is too large. This is probably due to the fact that good teams will put in their substitutes late in a game they know they have won, artificially making their statistics worse than those that produce victories, i.e. the floor%'s are not staying constant.
--Est'd-- Binom. Pyth16.5 Actual Team p_s p_ds Z* P(Z<Z*) Projexn Win% Atlanta .546 .542 .054 .522 .529 .524 Boston .552 .523 .411 .659 .708 .683 Charlotte .516 .543 -.372 .355 .306 .317 Chicago .563 .516 .653 .743 .806 .744 Cleveland .521 .534 -.177 .430 .403 .402 Dallas .519 .543 -.330 .371 .323 .341 Denver .516 .563 -.719 .236 .192 .244 Detroit .530 .513 .238 .594 .634 .610 Golden St. .549 .542 .113 .545 .558 .537 Houston .527 .509 .246 .597 .634 .634 Indiana .549 .551 -.028 .489 .486 .500 LA Clippers .506 .523 -.241 .405 .368 .378 LA Lakers .547 .513 .485 .686 .747 .707 Miami .500 .530 -.420 .337 .280 .293 Milwaukee .538 .526 .176 .570 .596 .585 Minnesota .520 .541 -.284 .388 .346 .354 New Jersey .504 .526 -.316 .376 .330 .317 New York .527 .528 -.017 .493 .491 .476 Orlando .519 .539 -.279 .390 .352 .378 Philadelphia .531 .531 -.013 .495 .493 .537 Phoenix .552 .521 .457 .676 .726 .671 Portland .553 .511 .604 .727 .786 .768 Sacramento .501 .536 -.489 .312 .246 .305 San Antonio .529 .507 .318 .625 .670 .671 Seattle .538 .532 .088 .535 .548 .500 Utah .534 .517 .239 .594 .631 .659 Washington .504 .529 -.351 .363 .312 .366
The Pythagorean projections listed in Table II come from the formula
P[win] _ (Points)^16.5/[(Points)^16.5+(Points Allowed)^16.5] 6
which was derived empirically from a fairly small set of data several years ago. The derivation simply involved looking at 53 good teams and 53 bad teams between the 1979-80 season and the 1986-87 season and determining the best exponent. The 53 good teams all won at least 48 games in a season and scored 486,483 points, allowing 465,093 points. Their cumulative winning percentage was 0.676, with a record of 2938-1408. The 53 bad teams all won 34 or fewer games, scoring 462,075 points and allowing 483,080 points. Their cumulative winning percentage was 0.324, with a record of 1407-2939. Teams that won between 35 and 47 games were considered close enough to 0.500 that a wide range of exponents in the Pythagorean formula would work. The exponent that fits this data best is about 16.5 and it has since been used exclusively in private work.
Manley examined this formula in his '89 Basketball Heaven book. Manley split up 161 teams from '80-81 to '86-87 into ranges of wins; for example, from 0-19 wins there were five teams, from 40-44 wins there were 31 teams, etc. He tested the Pythagorean formula on each range looking for the best exponent. What he found was that 16.1 was the optimal exponent for the entire group, but that the optimal exponent varied with how good or bad teams were. (See Table III) The best and worst teams showed the highest exponents, while teams closer to average showed smaller exponents. What the 'correct' exponent is will not be debated here because, in fact, the Pythagorean formula is not based on any solid theory. In a sense, it acts as an approximation to a normal distribution over a certain range of values (equations 5 and 6 describe the same thing), meaning that something could possibly be derived, but that is not the purpose here.
Number Total Best of wins Teams Exponent 60+ 12 17.6 55-59 11 15.1 50-54 16 18.5 45-49 22 12.6 40-44 31 3.7 35-39 23 10.7 30-34 17 16.1 25-29 16 16.0 20-24 8 17.1 0-19 5 18.8 161 16.1 From personal correspondence with Manley, 1988.
In Table II, notice that the Pythagorean projections for the '90-91 teams tend to be too exaggerated, i.e. too far from 0.500. This is somewhat surprising given its empirical derivation.
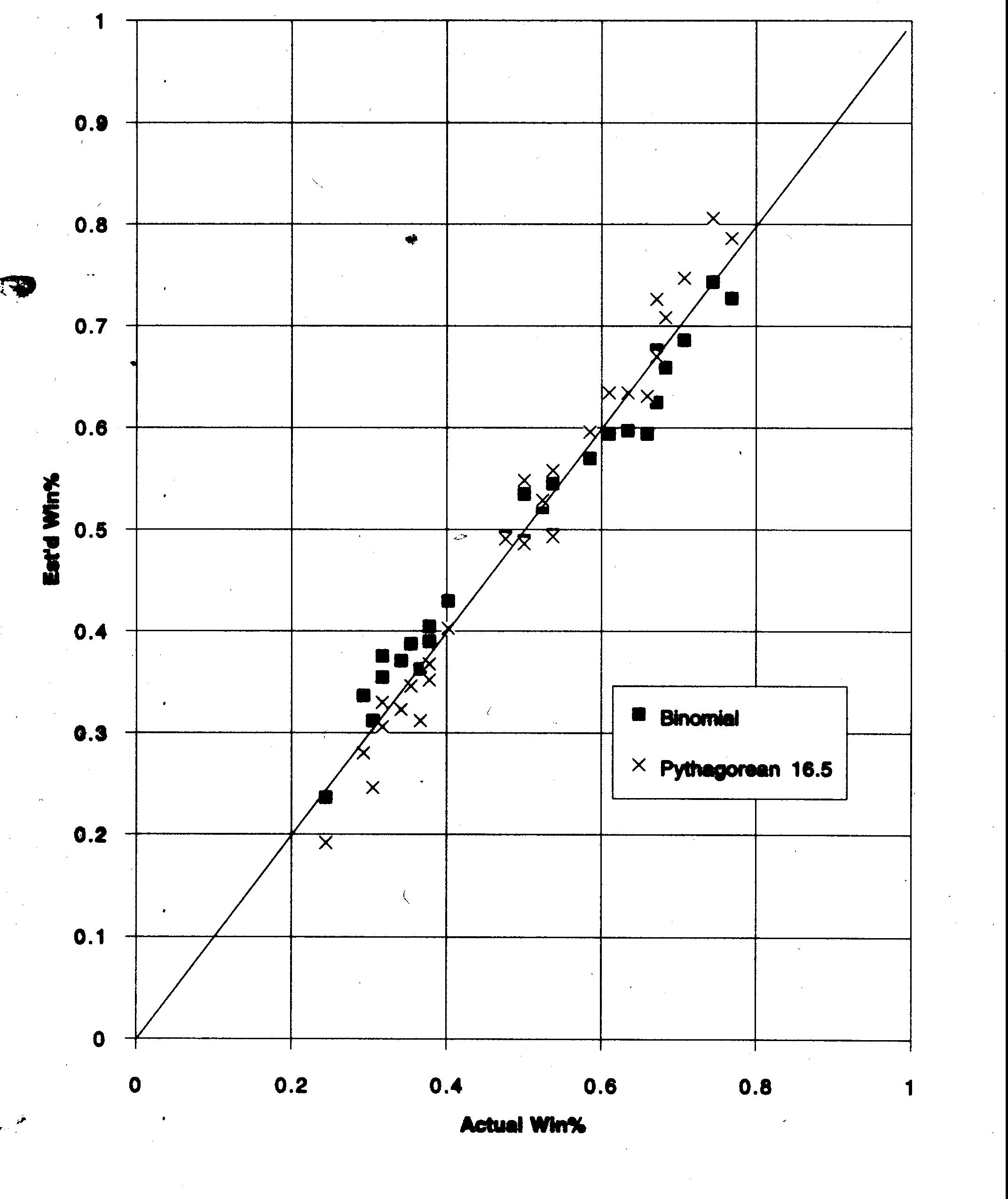
In Figure 2, we plot the binomial and Pythagorean projections versus actual winning percentages. Perfect prediction would put points on the 45° line shown. Notice that the two methods tend to put points on opposite sides of the line, showing graphically that the Pythagorean method predicts too wide a variation in winning percentages and the binomial predicts too small a variation. The mean-square difference between the binomial prediction and actual record is slighltly smaller than that between the Pythagorean and actual record. Even though this is just one season, this is impressive because if the true binomial formula (Equation 4) had been used and the value of a were adjusted away from 0.500 for each team, which it should be, the predictions from the binomial would have been more accurate.
The scoring method described here has tremendous value in modelling the game of basketball. Because it follows the ball from player to player, recording sequential occurrences in a game, it gives much more information than the traditional cumulative statistics. This method clearly demonstrates alternating possessions for teams, providing a method for determining offensive and defensive quality through offensive and defensive floor%'s and points per possession stats. These statistics are better measures of quality than simple points per game stats because they remove the bias for pace; running teams typically have higher points per game values both offensively and defensively than slow teams. Though no one has measured floor%'s or points per possession for a complete season, they can be estimated simply from equations 1-3. This scoring method and these approximate equations should have great value in analyzing the game of basketball.
We took advantage of the alternating possessions demonstrated in the scoring method by constructing a simple binomial model to estimate winning percentages. Though this model is overly simple and tends to overestimate the variance of scoring possessions, it showed results as good as those of the empirically derived Pythagorean Formula for the 1990-91 season.
Albright, S. C. 1978. A probabilistic model of winners' outs versus losers' outs rules in basketball, Operations Research 10, 1010-1019.
Cover, T. M. 1977. An offensive earned-run average for baseball, Operations Research 25, 729-740.
Freeze, R.A. 1974. An analysis of baseball batting order by Monte Carlo simulation, Operations Research 22, 728-735.
Heeren, D. 1990. Basketball Abstract 1991, Prentice Hall, Englewood Cliffs, NJ.
Heeren, D. 1988. Basketball Abstract 1989, Prentice Hall, Englewood Cliffs, NJ.
James, B. 1984. Baseball Abstract 1984, Ballantine Books, New York.
James, B. 1985. Baseball Abstract 1985, Ballantine Books, New York.
James, B. 1986. Baseball Abstract 1986, Ballantine Books, New York.
James, B. 1987. Baseball Abstract 1987, Ballantine Books, New York.
James, B. 1988. Baseball Abstract 1988, Ballantine Books, New York.
Lindsey, G.R. 1959. Statistical data useful for the operation of a baseball team, Operations Research 7, 197-207.
Lindsey, G. R. 1963. An investigation of strategies in baseball, Operations Research 11, 477-501.
Manley, M. 1987. Basketball Heaven 1988, Facts Publishing Co., Topeka, KS.
Manley, M. 1988. Basketball Heaven 1989, Facts Publishing Co., Topeka, KS.
Manley, M. 1989. Basketball Heaven 1990, Doubleday, New York.
Pankin, M. D. 1978. Evaluating offensive performance in baseball, Operations Research 26, 610-619.
Thorn, J. and Palmer, P. 1985. The Hidden Game of Baseball: A revolutionary approach to baseball and its statistics, Doubleday, Garden City, NY.
Thorn, J., Palmer, P., and Routher, D., Eds. 1991. Total Baseball, Second Edition, Professional Ink, Inc., New York.
Trupin, J. and Couzens, G. S. 1989. Hoopstats: The Basketball Abstract, Bantam Books, New York.