Making Your Teammates Better: Measuring It for the First Time

October 13, 1996

Constructing a successful team is not as simple as putting together good players. Many assemblages of talented individuals have failed to reach their goals because of what is often labeled as a "lack of chemistry". Though one can extend metaphors too far, this "chemistry" metaphor makes sense. The classic subject of chemistry involves evaluating how all the substances on earth interact: What happens when you put metal into an acid? What happens when you light a fire around hydrogen (kids, don't try this at home)? Sometimes, chemists put substances together and nothing happens; they're left with a mixture of the things they put together. Other times, they end up with a remarkable new compound made up of the original materials but in a complex and intricate way. And then sometimes, they blow up their laboratory in a magnificent display of carelessness and ineptitude.

Basketball (and team sports in general), like chemistry, involves evaluating how various things interact. Unfortunately, like most complex subjects, basketball has traditionally been analyzed piece by piece, player by player, offense vs defense, without clear regard for how those pieces, those players, affect one another.

This article, as far as I know, marks the first attempt at examining in detail the interactions that make basketball an exciting and complex team sport.

The general principal I will follow is to look at the relationship between an individual's performance and that of his teammates. If a player does well, do his teammates also do well? Clearly for a player like Michael Jordan who commands so much attention from the defense, this must be true and this research leads to one number that supports this.

As I explore the extent of this new method, I am finding that its results can be also be used to evaluate coaches and how their teams function. For those of us in the business of evaluating players, this method also raises serious questions about the use of traditional individual statistics like TENDEX .

In this article, I plan to explain a bit about the theory of the method with a few results. Over the course of the season, I will dig into this method much more and produce more results. Right now, the method is still new and not completely automated. It will be. It's that important.

Theory: What To Measure?

The way I intend to do this is, for every game, evaluate every player's offensive rating (points created per 100 possessions) and floor percentage (percentage of possessions used on which he scored) and compare each of these numbers to those for their teammates' in that game. For instance, on April 20, 1993, Michael Jordan had an offensive rating of 128.3 and his teammates had an offensive rating of 127.9, both very high numbers leading to a 123-94 win over Philadelphia. His floor percentage was 0.572 and that of his teammates was 0.590. Generally, the Bulls ran roughshod over the 76ers' defense. In a game 11 days earlier against Atlanta, Jordan had an offensive rating of 101.3, whereas his teammates had an offensive rating of only 89.4 in a one point win. Clearly, Chicago faced a better defense against Atlanta than they did against Philadelphia and it influenced Jordan as much as it influenced his teammates.

What I plan to do is to evaluate how much, on average, Jordan's numbers fluctuated with his teammates. In other words, I will look at the statistical correlation between Jordan's offensive ratings and those of his teammates. For those not familiar with statistics, I will explain a little. A correlation of 1.00 means that if Jordan's rating goes up by 12 and his teammates' rating goes up by 6, then if Jordan's rating goes down by 4, his teammates' rating goes down by 2; it's a simple relationship. A correlation of 0.00 means that Jordan's offensive rating tells us nothing about his teammates' rating. A correlation of -1.00 means that if Jordan's rating goes up, his teammates' rating will go down in a simple relationship. Typically, the correlations you will see will be between -0.10 and +0.50. These correlations indicate that what one player does only gives us partial information about how the rest of his team does. Correlations that are larger than zero mean that the player generally plays better when his teammates play better and plays worse when his teammates play worse. Correlations that are less than zero mean that the player generally plays better when his teammates play worse. Correlations that are closer to zero indicate players whose games are more independent of their teammates.

Note that there is no explicit cause and effect in these correlation numbers. In other words, a high correlation with your teammates does not mean that you "carried your team." Jump shooters who rely upon open shots being created by other players on their team may also have a high correlation with their team. This is something that will have to be evaluated as the method matures. On to some numbers...

Results of the Method

Since I have talked about Michael Jordan so much, let's start with him. I compared Jordan's 1993 offensive ratings from every game to those of his teammates and found a 0.32 correlation. This value, I am finding, is fairly high. Does this mean that Jordan helps his teammates do better? Well, it means that when Jordan is better than his average his teammates are generally better than their average. It also means that when Jordan is worse than his average, his teammates are generally worse than their average. It also may imply that, since Jordan's average numbers are so good (Jordan's 1993 season offensive rating was about 120.2 and his floor percentage was 0.581), he made the Bulls players better than they would be on another team. This is bolstered by the fact that Jordan's offense was consistent from game to game: his standard deviation of his offensive rating was 16.8 and of his floor percentage was 0.078, meaning that most of the time (about 68% of the time), his offensive rating varied between 103.4 (=120.2-16.8) and 137.0 (=120.2+16.8).

Let's look at the entire championship Bulls team from the '92-93 season. What follows is a table showing the correlation of each of the Bulls' players to their teammates, using both their offensive ratings and their floor percentages:

Correlations Between Individuals and the Rest of Their Team
	Rating	Floor%
Armstrong	0.11	0.15
Cartwright	-0.03	0.00
Grant	0.19	0.13
Jordan	0.32	0.24
King	0.02	0.01
Paxson	0.34	0.36
Perdue	0.20	0.21
Pippen	0.27	0.25
Williams S	-0.06	-0.08

As mentioned above, notice that the correlations are relatively small, none above 0.34. 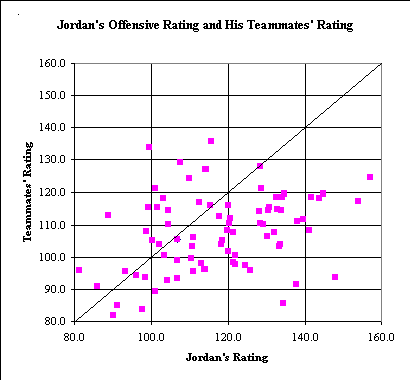I plot here Jordan's offensive ratings and those of his teammates throughout the season; Jordan's offensive rating is across the horizontal axis and his teammates' rating is plotted in the vertical. For example, look at the farthest right point: it indicates a game where Jordan had an offensive rating of about 157 and his teammates had a rating of about 125. You can see that there is a lot of scatter in this plot, but that there is evidence of Jordan's 0.32 positive correlation. Specifically, you can see that Jordan's greatest games (when his rating was up around 160), the rest of the Bulls also did well. When he was "average" (for him), his teammates could be great or could be mediocre. When Jordan was "bad" (for him), his teammates were also below average. This implies a general strategy that says, "Stop Jordan and you stop the Bulls". These stats alone do not support this strongly, but they certainly do not support the alternative theory, "Stop Jordan's supporting cast because Jordan can't beat you by himself."

As a secondary note, the above table indicates that the Bulls' "goons" in the middle -- Bill Cartwright, Stacey King, and Scott Williams -- weren't really correlated with the rest of the team. This is a sign that they weren't a large part of the offense. I also wonder whether it had to do with the Bulls' triangle offense, a question I hope to eventually answer with more recent data.

Following up with the Jordan comment, there is a way to roughly identify whether Jordan "carries" the Bulls. This is by looking at whether he consistently outperformed his teammates or whether they outperformed him... duh:

Percentage of Times Player Was Better Than His Team
	Rating	Floor %
Armstrong	65%	62%
Cartwright	40%	38%
Grant	51%	53%
Jordan	74%	73%
King	38%	46%
Paxson	53%	47%
Perdue	36%	43%
Pippen	47%	48%
Williams S	39%	44%

This shows that Jordan's offensive rating was better than his teammates' 74% of the time and his floor percentage was better than his teammates' 73% of the time. Now we know several things about Jordan's influence on the Bulls:

1. On average, Jordan's offensive numbers were very good.
2. Jordan's offensive numbers were consistent, never having a game where his rating was below 80 and usually being between 100 and 140.
3. Jordan's teammates generally played above average when Jordan played better than his average and worse when he played worse than his average.
4. Jordan consistently had higher ratings and floor percentages than his teammates.

Finally, I decided to look at how well each individual on the Bulls' team play with each of the others. The following table shows this by looking at the correlation of ratings and floor percentages. The way to read this table is to look for the column and row where the two players you are interested in intersect. In the Jordan column and the Paxson row, you can see that these two players played well together, having a correlation of 0.47 in their ratings and 0.48 in their floor percentages. I'll let you read the rest. (Players are perfectly correlated with themselves as indicated by a 1.00 in the cell where their column and row intersect.)

Correlations of Ratings and Floor Percentages Between Individuals
	Williams S		Pippen		Jordan		Grant		Cartwright		Armstrong		King		Paxson		Perdue
	Rtg	Fl%	Rtg	Fl%	Rtg	Fl%	Rtg	Fl%	Rtg	Fl%	Rtg	Fl%	Rtg	Fl%	Rtg	Fl%	Rtg	Fl%
Williams S	1.00	1.00
Pippen	0.04	0.02	1.00	1.00
Jordan	0.04	0.03	0.37	0.34	1.00	1.00
Grant	0.00	-0.04	0.17	0.12	0.01	-0.07	1.00	1.00
Cartwright	0.29	0.29	-0.05	-0.03	-0.03	-0.02	-0.07	-0.06	1.00	1.00
Armstrong	-0.14	-0.11	0.21	0.20	0.08	0.04	0.07	0.04	0.07	0.07	1.00	1.00
King	-0.12	-0.11	0.02	0.00	-0.14	-0.10	0.15	0.16	-0.05	-0.04	0.02	0.02	1.00	1.00
Paxson	-0.12	-0.10	0.21	0.26	0.47	0.48	0.05	0.03	0.05	0.07	0.12	0.13	-0.07	-0.08	1.00	1.00
Perdue	0.14	0.13	0.21	0.18	0.14	0.12	0.27	0.25	-0.10	-0.04	0.07	0.11	0.08	0.11	-0.03	-0.06	1.00	1.00

As a final comment, note that the starters were more correlated with one another than they were with bench players. And, as mentioned above, since the big guys generally had little correlation with other players, I have to wonder whether the Bulls' triangle offense helps keep all the starters positively correlated with the exception of the center.

Addendum

To Be Continued

Again, I wish to thank Rob Schoen for the use of his database.