There are a large number of statistical methods that have been developed to help study basketball. Most of these can be learned from context, I believe. However, there are a few methods that I feel are vital for the understanding and continued advancement of the studies of the game. These are the Possession Scoring System, a simple way of recording what happens in a basketball game; points per possession ratings; floor percentages; and the Correlated Gaussian Method.
The basis for a large number of the methods used herein is the Possession Scoring System, a method I developed for recording what happens in a basketball game. Although most readers can understand all articles presented in JoBS without reading the full description of this scoring system, they will find it much easier to expand upon results by understanding this system. Also, use of the system is important for developing better analysis tools and for increasing the data available for analysis. Finally, since many of the established analysis methods were derived from this scoring system, they will be easier to understand if the Possession Scoring System itself is understood.
The other two methods I referred to are ones that are derived from this scoring system: points per possession rating and floor percentage. A points per possession rating is exactly what it sounds like: points divided by possessions. It can be used for teams or individuals. If you want to know more, you can read about it below or by using the index in the frame to your left. A floor percentage will not be familiar to many people, but it is simply the percentage of possessions on which there is a score (of 1 point, 2 points, or more). It, too, can be used for teams or individuals. If you want to know more, you know what to do.
Other methods used here are similar to those found in the analysis of baseball, particularly those of Bill James, whose work popularized the study of statistics in sports because it was scientifically solid and entertaining to read.
First, the definitions and corresponding formulas, if applicable, then discussions on the subtleties, implications, and/or derivations of each term and the theory behind it.
(from the article A New Scoring System and A Binomial Model of Basketball)
(A good example of how this method can be used to replay a game is this excerpt from Game 4 of the 1997 Finals.)
The new scoring system we developed is not designed to replace traditional scoring methods, which are quick and efficient for tabulating cumulative statistics. This scoring system, known as the Possession Scoring System, was designed to collect as much information as possible about the game, which means giving up the simple tabulating techniques. All that is really needed to score a game using this system is something to write with, four sheets of lined paper (both sides will likely be used), and a decent understanding of basketball scoring rules. The NBA usually has several people working to keep official stats, but this method only requires one person. That one person, however, must work fast.
The System is very simple. It focuses on the player with the ball, following the ball from player to player until the ball is turned over to the opposition through a shot attempt or turnover. For example, a scoresheet for part of a Detroit-Los Angeles Lakers game might look something like this: [Editor's Note: In the original document, many of the following symbols were in subscripts or superscripts.]
23 LA 32D 4 42 4 32 ++B 22 D 11D 4D 53 ++L 24 LA 45D 32D 42 F10(2) xo 25 D 4D 40 11D +Y3pt 24 LA 32D 42D 4 21 -X 27 D 10R 4D 23 ++R FB 27 LA 32 45D 32D 45 32D -2 32R +L F40(1) o TIME 1:13 27 D 11D 53 11 15 TRVL TO 27 LA 32D 4D 42D -R BK22 27 D 11RD BP TO 29 LA 4STL D 32D 4++R FB 29 D 11D 4D 40 -A 11R +3 29 LA 32 -Y END 1Q
This brief section of a hypothetical scoresheet shows the end of the first quarter between Detroit and Los Angeles. The opening page of the scoresheet would note certain information about the teams, such as which is the home team, their starting lineups, who is favored, the game time, and any other relevant information. For instance, if it was Game 6 of the NBA Championship Series, it would be noted.
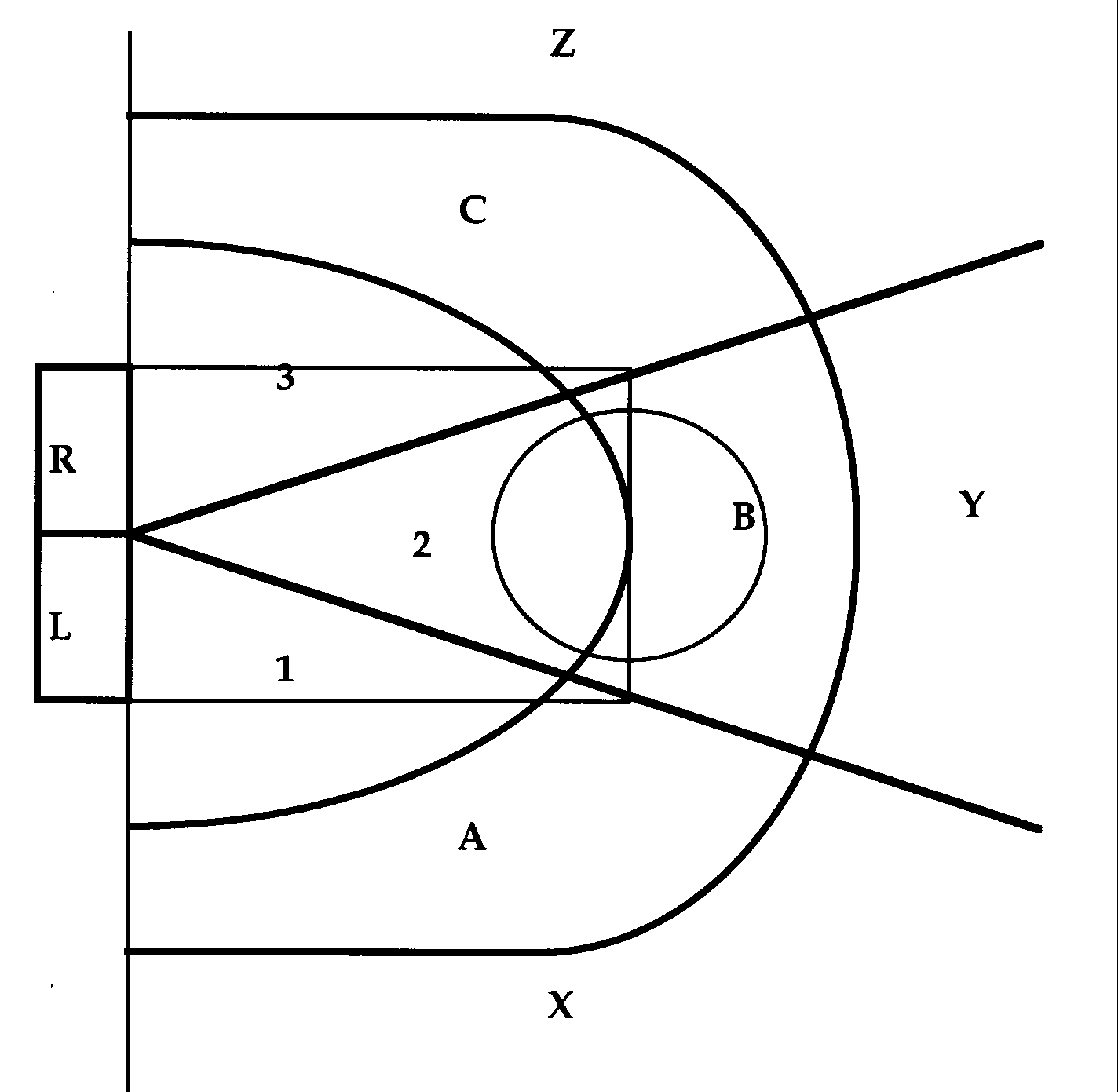
On the left is the running score of the game. On the first line, the number 23 appears to the left of 'LA', meaning that the Lakers ended the possession with 23 points. The numbers to the right of 'LA' or 'D' on each line correspond to the jersey numbers of the players as they touch the ball. For example, the first line shows that the Lakers' number 32, Magic Johnson, dribbled (32D), then passed to Byron Scott (number 4), who passed to James Worthy (number 42), who passed back to Scott (4), back to Johnson (32) who made a jump shot on the assist from Scott (4 32 ++B). [The complete Laker possession: 32D 4 42 4 32 ++B] A flat line (-) next to a number indicates that the person with that number shot the ball. If the flat line is crossed vertically (+), then the shot went in. If a second vertical line is present (++), then an assist - officially defined as a pass that "directly leads to a basket" - is credited to the player whose number is listed previous to the one who made the shot. The subscript next to the symbol indicating a shot is a shorthand for where the shot was attempted on the court. In this case, the subscript B means that Johnson took the shot from between the free throw line and the three point line in the middle of the court. All the regions of the court are seen in Figure 1.

On the second line, Detroit has the ball. Isiah Thomas dribbles (11D)
up the court, then passes it to Joe Dumars (4). Dumars dribbles (4D)
then finds James Edwards for a layup from the left side (53 ++L)
for the Pistons' 21st and 22nd points.
[The Detroit possession: 11D 4D 53 ++L]
Next, Los Angeles has the ball again. A.C. Green (45) this time dribbles
the ball up (45D), gives it to Johnson who then maneuvers for
a pass into Worthy. Worthy is fouled by Dennis Rodman, his second (F10(2)),
which sends Worthy to the line for two free throws. He misses the first
(x) and makes the second (o), giving the Lakers a 24-22 lead over the Pistons.
[Laker possession: 45D 32D 42 F10(2)
xo]
Then it's Detroit's turn. Dumars dribbles up, passes to Bill Laimbeer
(40), who then gives it up to Thomas. Thomas dribbles around, then takes
and makes a three point shot from straight-away (11 +Y3pt).
No assist was credited, so there is only one vertical line. Detroit leads
25-24.
[Detroit possession: 4D 40 11D +Y3pt]
Johnson brings the ball up for the Lakers next possession and passes
to Worthy. He dribbles, then finds Scott, who swings it to Michael Cooper
(21). Cooper misses his three point attempt from the left side (21 -X).
[Laker possession: 32D 42D 4 21 -X]
The missed shot is rebounded by Rodman (10R), who outlets
to Dumars streaking up the court. Dumars hits Mark Aguirre on the right
for a fast-break (FB) layup (4D 23 ++R FB).
[Detroit possession: 10R 4D 23 ++R
FB]
The Lakers get the ball, down 27-24. Johnson hands the ball to Green
to bring up the court. When Green reaches the front court, he finds Johnson
and Johnson dribbles around. He gets the ball back to Green so that he
can get himself free. Green gives it back to Johnson, who drives to the
basket and misses a shot from the middle of the lane (32D -2).
Johnson gets his own rebound (32R), puts it back up and in with
a foul on Laimbeer to help complete a three point play (32R
+L F40(1) o ). This ties the score at 27 and time
is called (TIME 1:13).
[Laker possession: 32 45D 32D 45 32D
-2 32R +L F40(1) o TIME
1:13]
Detroit's Thomas has the ball when play resumes. He dribbles up, passes
to Edwards, who passes it back to Thomas, who finds Vinnie Johnson. Johnson
travels and turns the ball over (15 TRVL TO). The ball goes back to the
Lakers with the score still tied at 27.
[Detroit possession: 11D 53 11 15 TRVL TO]
The Lakers' Johnson brings it up, finds Scott, who then dribbles trying
to free himself and/or pull the defense off Worthy. Worthy gets the ball
from Scott and puts it on the floor going for the layup, but John Salley
is there to block it away (42D -R BK22).
A wasted possession for the Lakers.
[Laker possession: 32D 4D 42D -R
BK22]
The ball goes back to Detroit via a Thomas rebound, who starts dribbling
up court looking for another break (11RD). He tries to sneak
a pass past Byron Scott, but instead turns it over on the bad pass (BP
TO).
[Detroit possession: 11RD BP TO]
After Scott's steal (4STL ), he dribbles up looking for a
Laker break. He finds Johnson, who then returns the favor by assisting
on a Scott layup (or dunk). The Lakers go ahead 29-27.
[Laker possession: 4STL D 32D 4++R
FB]
Detroit comes back looking for the last shot. Thomas dribbles up and
passes to Dumars. Dumars sees the clock running down and drives, kicking
it out to Laimbeer for a jumper from the left side. It misses, but Thomas
is in the right place at the right time for the rebound. He throws up a
high arcing shot from just outside the right side of the key and it falls.
Tied at 29.
[Detroit possession: 11D 4D 40 -A
11R +3]
Magic Johnson throws up a length-of-the-court shot to end the first
quarter. The score remains 29-all.
[Laker final possession: 32 -Y]
In this scoresheet, we tried to demonstrate most of the common situations in basketball. Some other common situations and how they are denoted: Jump balls are simply noted by the word 'Jump' and the numbers of the two players involved. Rebounds that go out of bounds are denoted by ROB. Sometimes it is necessary to note who is inbounding the ball; for instance, if number 22 inbounds the ball and commits a turnover on a bad pass: OB22 BP TO.
Recording all this information during a fast-paced basketball game is not easy, but it becomes fairly routine after practicing a few times. Often during the heat of a game, it is easy to forget to note things like fast breaks or blocked shots, but the fundamental structure of the system - noting who touches the ball and whether they shoot it or pass it - is not difficult to maintain.
An important thing to notice in this demonstration is how teams alternate possession during a game. In this example, the Lakers would score, commit a turnover, or not get a rebound, then Detroit would get the ball. For each opportunity that the Lakers get to score, the Pistons also get a chance. By getting an offensive rebound, a team is seen as 'keeping its opportunity to score alive' rather than 'creating another opportunity'. By scoring this way, possessions are equal for both teams in a game. Just as each team has the same 48 minutes in a game to outscore its opponent, each team also has the same 100 or so possessions in a game with which to outscore its opponent. [Note: This is the same way Albright (1978) defined possessions, but not how Manley (1988) defines them.]
One result of using this scoring method is that we can calculate probabilities of scoring for both teams over an equal number of trials. [Note: In a non-overtime game, it is possible that one team will have as many as two more possessions than its opponents. It appears unlikely, however, that any one team will consistently have more or fewer possessions than its opponents over the course of an 82 game season.] A scoring possession is defined as a possession on which one or more points are scored. A floor percentage (floor%) is then defined as the ratio of scoring possessions to total possessions. Over the course of a season, we can estimate the offensive floor%, ps, and the defensive floor%, pds.
For a team, it is the period of play between when one team gains control of the ball and when the other team gains control of the ball. For an individual, a possession or part of a possession is credited when that individual causes to end his/her team's possession.
This concept is simply envisioned for a team. It can be extended to apply to individuals as well.
Possessions=FGA-OR+TO+0.4*FTA
FGA=Field Goals Attempted OR=Offensive Rebounds
TO=Turnovers FTA=Free Throws Attempted
This possessions formula is for teams (there is a separate definition for individuals). When applied, a team's offensive and defensive (its opponents' offensive) stats are both run through the formula, then the average is taken. Almost without exception, the two estimates are within one percent of each other at the end of the season, making the averaging a safe procedure.
This is complicated and I will be adding the full details soon.
Without a doubt the most important term to understand thoroughly is possessions. There are two meanings of the term used in this business and it is often difficult to tell which one is which in normal conversation. One meaning is the one given here and the other is the following: "A team is said to have possession when it has uninterrupted and complete control of the ball. A possession ends when a field goal is attempted, when there is a turnover, on a jump ball, or after a free throw that is not the first of two."
Though the definitions are similar, there is one key difference. Under the former definition, teams alternate possession, while under the latter definition, a team can have consecutive possessions by getting an offensive rebound or by winning a jump ball after being tied up by the defense. With the former definition, opposing teams in a game will always have the same number of possessions (or be within two of each other), as happens with the Possession Scoring System. With the latter, a team that gets a lot of offensive rebounds will have more 'possessions' with which to score than their opposition if the opposition doesn't get many offensive rebounds.
The definition to get to know is the former one, which I'll call Definition A. In retrospect, I suppose that I could have done my research with the latter one (Definition B), but I did not and I believe it would have been less valuable as a tool.
The benefits of definition A become clear when using possessions to rate offenses and defenses, an invaluable exercise in getting to know basketball. Picture the two following situations: 1) A player brings the ball upcourt, takes a twenty foot jump shot and makes it. 2) A player brings the ball upcourt, takes a twenty foot jump shot and misses, but a teammate rebounds, misses the stickback, then gets his own rebound and finally puts in a layup. The first situation involves one scoring possession and one total possession regardless of which possession definition is used. The second situation has one scoring possession and one total possession using Definition A for possessions. Using the other meaning, the second situation involves one scoring possession and three total possessions.
Which situation represented the better offense? An offense's job is to score as many points as possible before the opponents take control of the ball (go on offense). If you can agree to that, then situations 1 & 2 represent offenses with equal efficiency. Both times the offense came away with two points before the opponents played offense. Looking at it another way, in the first situation, the offense did one 'good' thing (made one shot) and nothing 'bad'. In the second situation, the offense did three 'good' things (one field goal and two offensive rebounds) and two 'bad' things (two missed field goal attempts), netting one 'good' thing. Looking at end results ("the end justifies the means" is a great expression in this case), it can't be disputed that the situations represent offenses of equal quality.
Using the strict definition of floor %, scoring possessions divided by total possessions, efficiencies can be calculated for each situation for both meanings of possession. In the first situation, either definition of possession yields a floor % of 1/1= 100%. In the second situation, floor %= 1/1= 100% using Definition A of possessions and floor %= 1/3= 33% with Definition B. Agreeing above that both offenses are equal, floor % is not a useful measure of quality with Definition B possessions. As a matter of fact, it would be difficult to come up with a stat that used Definition B possessions in any way to truly measure quality. Therefore, you can forget Definition B possessions. All references to possessions hereafter are meant as Definition A possessions.
For a team, it is any possession on which at least one point was scored. For an individual, a scoring possession or part of a scoring possession is credited when that individual contributes to his/her team's scoring possession.
This concept is simply envisioned for a team. It can be extended to apply to individuals as well.
There are a few methods:
I generally calculate individual scoring possessions and sum them up, though this isn't practical if you need a rough first approximation.
This is complicated and I will be adding the full details soon.
Scoring possessions divided by possessions. The percentage of a team's or individual's possessions on which at least one point is scored .
This method applies in a straightforward manner to teams. The method is more complicated in applying to individuals because scoring possessions and possessions are more complicated to define for individuals.
There are a few ways:
This is complicated and I will be adding the full details soon.
Floor %, as already mentioned, is used to measure offensive efficiency. The not so obvious reason it can be used that way is because almost all scoring possessions for all teams involve two points being scored, not one point or three points. A normal game might have one team scoring on 58 of 100 possessions and the other scoring on 53 of 100 possessions. The team scoring on 58% of its possessions will win 99% of the time (that's an educated guess not based on scores of hundreds of games). The only ways the team with the 53% floor % will win is by making enough three pointers and/or by having several of the 58 opponent's scoring possessions be worth only one point (making only one of two free throws). A typical score for this game would be 116-106. It might be 114-108 or 117-105, but any difference smaller than about six points or larger than about fourteen would be very unusual.
It was originally intended to be an approximation to a team's floor percentage. Now it is only defined by its equation.
This method applies in a straightforward manner to teams.
Floor %= (FG+OR)/(FGA+TO)
Scoring possessions divided by possessions, omitting offensive rebounds. This serves as an estimate of how well a team scores if they never got an offensive rebound.
This method applies in a straightforward manner to teams.
Play %= [FG+0.4*FTA*(FG%*FG%+2*FG%*(1-FG%))]/(FGA+0.4*FTA+TO)
Points divided by possessions times 100. Also called simply "Rating", "Offensive Rating" for points scored per 100 possessions, or "Defensive Rating" for points allowed per 100 possessions. A related term is Adjusted Points per Game
This method applies in a straightforward manner to teams. It can also be applied to individuals, but the method is more complex.
Points per possession= Points scored or allowed/possessions
Offensive Rating= Points scored*100/possessions
Defensive Rating= Points allowed*100/possessions
This is complicated and will be explained here soon.
Points per possession is the best way available to measure the quality of offenses and defenses. The method takes into account points scored, field goal percentage, turnovers, offensive rebounds, and free throw percentage - everything (except for assists and, maybe, fouls) that can justifiably be looked at in measuring offensive or defensive quality. Possessions, as they were defined previously, make such a complete measurement possible. Repeating what is so important: When a team has the ball, its whole purpose is to score as many points as possible before it becomes the defense. If it were easily accomplished, teams would try to get fouled every time, miss the last free throw, get the offensive rebound, try to get fouled, miss the last free throw, etc., never having to play defense. Score lots of points in a possession and you are not giving the opposition a chance to catch up. The most common way to do that now is to score two points every time down the court. Points per possession shows which offenses do it best and which defenses stop it best.
In practice, points per possession (the number), is rarely used. Numbers like 1.071, which result by dividing points by possessions, are troublesome to handle with three numbers after the decimal and a leading 1. The overall rating (also called the study rating and points per 100 possessions) just multiplies points per possession by 100 to get aesthetically more normal numbers. It is often used in comparing offenses or defenses from different seasons. Adjusted points per game multiplies points per possession by the league average for possessions per team per game to reflect both the quality of the team and the average game pace in the league for that season.
As an example, the best offense of the '73-74 season was Milwaukee's with an offensive rating of 99.3, meaning that the Bucks and Kareem Abdul-Jabaar scored 99.3 points per 100 possessions. A normal NBA game in '73-74 had each of the opposing teams using 110.0 possessions to score their points. In such a normal game, the Bucks would score about 109 points (109.2 to be more exact) against an average defense. The Bucks actually employed a very slow pace that season, averaging only 107.9 possessions per game, meaning that they normally didn't score 109.2 points in a game. There were so many teams that had faster paces than the Bucks that seven teams scored more total points. But the Bucks did it better. Milwaukee led the league in field goal percentage and assists and did well in offensive rebounds. The Bucks' 99.3 rating, though it led the league would now be among the worst in the NBA. New Jersey had an offensive rating of 99.9, which was second to last in '87-88. Because the pace of the game is so much slower now, the Nets adjusted points per game rating was 101.7, much lower than the Bucks' 109.2.
Adjusted PPG is just points per possession times the league average of possessions per team per game. This scales its yearly average to be the same as the league average for PPG.
This method applies in a straightforward manner to teams. It has never been applied to individuals.
Adjusted field goal percentage is just a real simple modification of field goal percentage that gives proportional extra credit for making three pointers. It has special uses for three point specialists and also helps to identify where a problem might be in a team's offense.
An adjustment made to field goal percentage giving three-halves credit for three point shots made. It adjust field goal percentage by the weight of three pointers to two pointers.
This method applies in a straightforward and similar manner to both individuals and teams.
Adj FG%= (Total FG+0.5*3ptFG)/Total FGA
A method that gives an expected winning percentage using the fact that the ratio of a team's wins and losses is related to the number of points scored by the team raised to some exponent, which is usually taken to be 16.5. Other methods use 13, 16.1, or 17.
This method applies in a straightforward and similar manner to both individuals and teams.
Expected Winning %=(Pts scored)^(16.5)/[Pts scored^(16.5) + Pts allowed^(16.5)]
or, equivalently,
Expected Winning %=(Off. Rating)^(16.5)/[Off. Rating^(16.5) + Def. Rating^(16.5)]
The Pythagorean Method for relating points scored and allowed to wins and losses is an approximation to a more theoretically correct method, called the Correlated Gaussian Method. Both methods are used in JoBS, but it is hoped that the Correlated Gaussian Method will be used more in the future.
The Pythagorean 16.5 Method was derived from the corresponding method in baseball used by Bill James. 'Derived' may not be the proper word because I'm not sure if I knew what I was doing when the formula came out. You see, the corresponding baseball formula is identical to the basketball formula except that the exponents are 2's instead of 16.5's. What the derivation entailed was estimating average margins of victory for both sports and playing around with the logarithm button on a calculator. The number 16.76... came up on the first try. My expectations were for something between 13 and 20, so 16.76 was originally rounded up to 17 and tested as a valid possibility. It was then replaced by 16.5 after a more thorough empirical study. Martin Manley looked into this issue and came out with 16.1 as the exponent. I saw someone else use 13 as the exponent. I use 16.5 through most of JoBS, but that will be changing due to the development of the Correlated Gaussian Method for doing the same thing as this does.
The principle behind the method - that a team's won-loss record is closely related to the number of points it scores and allows - should be no surprise. It just makes sense that teams that win 60 games outscore their opponents by more than teams that win 50 do. However, one of the things that the Correlated Gaussian Method has added is that consistency also plays a role. Teams that win 60 games do not have to outscore their opponents by more on average than teams that win 50. They just need to be more consistent from game to game.
On the other hand, luck resulting from 'well-timed scoring' is a weak force in the NBA. It doesn't separate the good teams from the bad teams; it just separates two teams of similar quality. Taking the luckiest and unluckiest teams in the NBA, we usually find a total deviation of 10 to 13 wins. Luck has a place in basketball, just as the weather has a place in football and as Wrigley Field has a place in baseball. Each has an effect on the game, but, in the long run, the better teams win with or without the advantage or disadvantage of such factors. (In the short run, like the playoffs, luck can be pretty important. Witness the 1995 Houston Rockets.)
Occasionally luck plays a major part in a team's season. The '85-86 Clippers won 32 games, while their point totals led to an expectation of only 21 wins. A third of their victories (!) came out of the Twilight Zone. The '86-87 Clippers came back to reality, going through a pitiful 12-70 season in a daze. The '86-87 Warriors exceeded their Pythagorean projection by eight games, winning 42 instead of 34 games. They, too, crashed the following season, winning only 20. Both the Clippers and Warriors lost key personnel in their follow-up seasons, but neither ever showed any signs of life anyway. This sort of collapse can be seen throughout the history of basketball, but it's also seen in baseball (and probably other sports). The baseball people called this the Johnson Effect. It's the same effect in basketball so it gets the same name.
A method that relates winning percentage to points scored, points allowed, the standard deviations of points scored and allowed, and the correlation between points scored and allowed. Points scored can be replaced with offensive rating and points allowed can be replaced with defensive rating.
This method applies in a straightforward manner to teams and probably applies in a similar manner to individuals.
__ __
| (Rtg-Opp.Rtg) |
Win% = NORM |-----------------------------------|
| SD(Rating Difference) |
-- --
SD(Rating Difference) = SD(Rtg - Opp.Rtg)
= SQRT[Var(Rtg)+Var(Opp.Rtg)
-2*Cov(Rtg,Opp.Rtg)]
NORM means to take the percentile of
a mean-zero variance-one normal distribution
corresponding to a value given by that in
the brackets I faked.
Rtg: Points scored per 100
possessions (offensive rating)
Opp.Rtg: Points allowed per 100
possessions (defensive rating)
SD(): Statistical standard deviation
of quantity in parentheses ()
Var(): Statistical variance of
quantity in parentheses ()
Cov(): Statistical covariance of
quantities in parentheses ()
This method can be found in Microsoft Excel as NORMSDIST(z).
Given a value of z, this function evaluates what percentage
of a Normal (or Gaussian) Distribution is smaller than z.
See Basketball's Bell Curve for a discussion of this method. It has also been used in other articles, such as The Effect of Controlling Tempo and What Strategies Are Risky?
This method accomplishes the same thing as the Pythagorean Method, providing more insights, but also requiring more information.
This is a very useful method for determining how often Team A, with a winning percentage of X, will beat Team B, with a winning percentage of Y. It can be modified to account for other factors, such as home court advantage, etc. (This all comes from Bill James' Baseball Abstracts.)
This method applies explicitly to teams, but there is no obvious reason that it cannot be applied to individuals once winning percentages have been evaluated for them.
In a 0.500 league, i.e., where all we have are the overall records and no information about home court advantage, etc.:
Win%A_B = [Win%A*(1-Win%B)]/[Win%A*(1-Win%B)+(1-Win%A)*Win%B],
where Win%A_B is the chance that A will beat B, Win%A is A's winning percentage against the league, and Win%B is B's winning percentage against the league.
In a non-0.500 league, things are different. For example, if Team A is the home court team and Win%H is the percentage of times the home team wins, we have
Win%A_B = [Win%A*(1-Win%B)*Win%H]/[Win%A*(1-Win%B)*Win%H+(1-Win%A)* Win%B*(1-Win%H)]
For example, say the Lakers are 8-2 and the Celtics are 5-5 and they are playing on the Lakers' court. The league's home court teams win 60% of the time. Then, ignoring the home court advantage, we estimate the Lakers' chance of beating the Celtics as (0.8)*(1-0.5)/[0.8*(1-0.5)+ (1-0.8)*0.5]=0.8, or 80%. Incorporating the league home court advantage gives the Lakers' chance of winning as (0.8)*(1-0.5)*(0.6)/[0.8*(1-0.5)*0.6+(1-0.8)*0.5*(1-0.6)]=0.857, or 85.7%.
This method approximates the winning percentage of a team using a binomial distribution and its properties. A basic outline of the concept is in this paper.
This method currently applies only to teams.
A baseball (sabermetric) term that has applications in basketball. It states: "The tendency of teams that exceed their Pythagorean projection for wins in one season to relapse in the following season." (From The Baseball Abstract)
This theory applies only to teams.
The tendency for teams that improve or decline by a significant number of games from one season to another to rebound in the original direction the following season.
This theory applies only to teams.
An integer estimate of a player's value, making no fine distinctions, but, rather, distinguishing easily between very good seasons, average seasons, and poor seasons. There are two ways to calculate approximate value (AV). One uses rules and is explained below. The other is based on a statistic devised by Martin Manley called credits. Both methods produce essentially the same results.
These methods have been applied only to individuals.
The formula for credits comes from Martin Manley. It is very similar to other linear methods, such as Tendex, HoopStat Grade, and all the other flavors of linear weights floating around, some using the name Tendex (poor Dave Heeren). I would suggest that we can modify any of them for use in my AV method, but I haven't done it. Nor will I likely do it since I think they are all approximations and any argument for or against any of them having to do with accuracy is pointless.
Credits= PTS+REB+AST+STL+BLK-FG MISSED-FT MISSED-TO
AV= Credits^(3/4)/21
Before the '73-74 season, steals (STL), blocks (BLK), and turnovers weren't kept as official stats. In the credits formula for player seasons before '73-74, those stats are just omitted as they tend to cancel each other out to some degree when included anyway.
If a player makes first team or second team All-Defense, then one point is added to AV.
The Value Approximation Method was a major task to come up with, taking me about two months to finally arrive at satisfactory results. The plan for the method was to end up with a scale of integers between 0 and about 20 rating players, with 10 representing an 'average' player. It was to be based upon several standards a player was to meet in order to gain points of approximate value. The whole thing was modeled on Bill James' Value Approximation method for baseball. As James did, I assigned verbal descriptions to ranges of scores in order to see if the method produced results that matched general descriptions of players. Those descriptions are as follows:
After all the work to produce rules and standards that would fit the above descriptions, Martin Manley soon came along with a better method to approximate basketball players' values. He called it a Production Rating. Production Rating (PR) was defined by him as credits (as defined by formula earlier) per game. I fooled around with PR a little in hopes of deriving a points created formula, but soon found it to be a fruitless task. Instead, a simple way to calculate approximate values came out.
AV= Credits^(3/4)/21 + 1 if All-Defense
In my conversations with Mr. Manley about this manipulation of his method to fit the verbal descriptions and range of scores above, he pointed out a couple of things. First, he thought that instead of using credits, a player's PR*82 should be used. For players who played a full 82 games, there would be no difference, but for players like Magic Johnson or Adrian Dantley last year, who missed quite a few games, there might be a difference of about two on the AV scale. His reasoning for this suggestion was that "stats on a per game basis is so basketballish whereas total season stats are so baseballish...no one cares how many total points Jordan scored [in '86-87] - only that it was 37.1 per game." The second suggestion Mr. Manley made was that the conversion be simpler, dividing credits by 130 rather than raising credits to the 3/4th power and dividing by 21.
Both suggestions have their merit, but there are reasons not to implement them. His first suggestion to replace credits with PR*82 I hesitate to use for one main reason. While per game stats may be more 'basketballish', they do not represent a player's total value to his team over a whole season, which is what AV tries to measure. No matter how good a player is, if he isn't playing, he isn't contributing to wins and isn't valuable to his team. In the ten games Magic Johnson missed last season, he did not contribute anything to the Lakers (at least nothing we can measure). In those ten games, someone else (Wes Matthews or Milt Wagner) came in to contribute. In a game, Magic Johnson contributes more to the Lakers than Matthews or Wagner does, but, in those ten games, Johnson's value was 0, while the other two put points on the board and were valuable to the Lakers. Potentially, Johnson's value was a lot more than Matthew's or Wagner's, but, to use a cliche (sorry), potential never won a game for anyone. Ask the coaches of Dennis Hopson, Chris Washburn, Benoit Benjamin, Reggie Williams, Ralph Sampson, Darryl Dawkins, Kent Benson, J.B. Carroll, Mychal Thompson, Len Bias or any player who ever had the 'potential' to be one of the best.
Mr. Manley's second suggestion comes down to simplicity and a little more. Dividing by 130 is simpler than doing what I do until you realize that all conversions are unnecessary once ranges of credits are written next to the corresponding AV. (Heck, we do everything with computers these days anyway! What's the big deal?) From 562.5 to 702.8 credits, the corresponding AV is 6. From 702.9 to 850.5, the corresponding AV is 7. Calculate credits, look on a chart for corresponding AV. That's simple enough. Numerically, the conversion methods don't differ too much until you get to great players with high numbers of credits. Wilt Chamberlain's '61-62 season gives an AV of 25 using the method in this book and an AV of 32 using Mr. Manley's suggestion of dividing by 130. Both are tremendous values and there is almost no reason to argue over the difference because Wilt's '61-62 season was clearly the best ever statistically. What it comes down to is this: the best baseball player ever, Babe Ruth, racked up AV's (using James' method) around 25-27 and if we say that Chamberlain dominated his sport as much as Ruth did his ("Chamberlain was the Babe Ruth of basketball"), then their best AV's should be about the same.
The purpose of the Value Approximation method is to quickly produce a useful number that represents the sum of all of a player's obvious contributions. In studies involving large groups of players, AV's are the most convenient way to quantify approximately how valuable the players are. If we wanted to find out how well a team drafts, we could add the career AV's of all the players they've drafted and compare that to the total for other teams. If we wanted to find out what position in the NBA was the position with the most valuable players, we'd use AV's and we might see how this compares with the NBA of 15 years ago. If we wanted to find out how productive the bench is on NBA teams, we might use AV's. There are many studies waiting to be done that could use the Value Approximation method to make them a little easier.
Linear weights is the name given to methods whose purpose it is to estimate points produced and that do it by adding a player or team's positive factors and subtracting a player or team's negative factors, with appropriate weights added to each of the factors.
These methods apply to both teams and individuals.
PtsCreated = a*PTS+b*AST+c*OR+d*DR+e*STL+f*BLK -g*TO-h*(FGA-FGM)-i*(FTA-FTM) -j*PF-k*FF-l*DQIn some versions of this formula, the result is scaled by a factor that accounts for whether the team (or the player's team, if it's applied to a player) played at a faster or slower pace than normal. I generally assign the value of 1 to each of the weights, a through i, and 0 to the others.
There is some valid debate in baseball over whether linear weights are appropriate for that game. I have little doubt that they are not appropriate in basketball, except as an approximate value method.
Linear weights are a simple way to approximately account for a large number of things a player does, both positively and negatively. Because they are simple and because they account for a large number of things, I use them in my approximate value method. However, as an instrument to study strategy or detailed aspects of the game, linear weights are generally inadequate. For one thing, the game of basketball is not linear, meaning that an increase in a positive statistic does not lead to a constant increase in points or wins, even in an expected value (probabilistic) sense. There is a statistical correlation between, say, blocks and points, but do we have any good reason to believe that 10 blocked shots in a game will mean twice as many points to our team than 5 blocked shots will? Even if it did "mean twice as many points", why is this simply added to the linear weights formula since blocks contribute defensively to taking away potential points allowed? Just by the fact that various people have assigned different weights to each of the components indicates that either the weights are not very well known or that they change for different people or teams (making it nonlinear) -- both cases invalidating the use of the tool for analysis.
That being said, linear weights are ideal for approximate value methods, which are great for performing studies involving large numbers of players and their overall contributions. For example, studying trades or free agent signings over a period of time or for many teams can use approximate value methods. A general look at the development of players as they age might use linear weights.
An estimate using a player's age and his approximate value to determine how much value a player has left in his career.
This method applies only to individuals.
Y= 27-0.75*Age
Trade Value= (AV-Y)2(Y+1)AV/190 + AV*Y2/13
A player's Y factor represents an estimate of how many seasons he has left to play and is always assumed to be at least one and a half years.
Another application of AV's is in the determination of trade values. Trade values, because they take into account both age and production, can be a good indicator of the future success of a team. Teams like Chicago, Cleveland, Sacramento, Portland, New York, and Seattle are all young clubs with high trade values and seem to have good futures. Teams like Denver, Detroit, Milwaukee, and, of course, Boston seem to be facing bad years within the next three years or so as they see their best players turning a little gray and their young players not producing.
Trade value will probably be an important part of one of my more ambitious (and unrealistic?) projects for the future, which is to devise a method that would give an approximate percent chance that a certain team will win a championship in one year, two years, three years, etc. Every year, magazines and newspapers give us their predictions for the coming season and they can be fairly accurate. Teams like New York and Cleveland that have so much young talent inspire questions about a more distant future, though. Of course, the farther in the future you look the less detail you can see and basketball predictions are an uncertain 'science' to begin with. Predictions, though, are an inevitable and unavoidable part of studying basketball from the point of view I've taken. The test of real sciences - physics, biology, chemistry - is not how well they can explain things that have already happened, but whether they can predict outcomes of future experiments. That is the general direction some of the research herein is going. Predictions may in fact be self-defeating because of the psychology involved, but they're worth trying.