The Effect of Controlling Tempo
17 February, 1996
What does a team gain by controlling tempo? Usually, when a
broadcaster says a team needs to control tempo, they are talking
about the team that doesn't like to run. Not always, but
usually. This was especially true in the '80's when the slow-down
East teams had to "control tempo" when playing the go-go
West teams.
Controlling tempo, in my mind, means not forcing a quick shot
after you've gotten beaten on a fast break. Basically, it
means playing smart basketball. Most teams at the college
or pro level can run and can play a half court offense, with
only marginally differing ability between the two. Unless
they are playing a team coached by Rick Pitino, whose teams
have traditionally forced a tempo, they run when the opportunity
is there and run a set offense otherwise. The times that
teams start to play at their opponents' tempo is when they
rush to get a shot off. Can you think of another time that
broadcasters criticize a team for not playing at their own
tempo?
Well, yes. Teams that like to run, but get stuck in a half
court game are described as not playing at their own tempo. But
this often (if not always) happens because their defense
isn't forcing the turnovers or getting the defensive
rebounds it needs to push the ball up the court. It also means
the opposition is scoring a lot. Running teams
don't force the ball up the court after a made basket
very often any more. Some did prior to this decade, like
the Lakers in the pros and that Loyola Marymount team
of the late '80's. But did that really help them stay
at their tempo and win the game?
My general feel on this issue is that teams slow down during
the playoffs and in important parts of games. They isolate
their best scorer and let that person score at their own pace.
I have seen and measured a dramatic slow down in playoff games
going back at least as far as 1988 when the Lakers were near
the end of their run as Champions. When the Pistons slowed
the game down, they seemd to do better against the Lakers.
It took a year, but that strategy finally paid off when the
Pistons swept the Lakers in '89, a series that was marred by
injuries to the two Laker starting guards.
What this has lead to, along with the article,
Basketball's Bell Curve,
is a theory that slowing down the game can help an
underdog win. It's more than a theory, actually, because
the method outlined in
Basketball's Bell Curve
and described in
New Measurement Techniques
and A Binomial Model of the Game of Basketball,
demonstrates how this can be true. The general
formula for estimating the probability that a team
is going to win is
__ __
| (ORtg-DRtg) |
Win% = NORM |------------------------------------------|
|SQRT[Var(ORtg)+Var(DRtg)-2*Cov(ORtg,DRtg)]|
-- --
where SQRT means to take the
square root of the quantity in the brackets and
NORM means to take the percentile of
a mean-zero variance-one normal distribution corresponding
to a value given by that in the brackets I faked, Rtg and
Opp.RtgG are the points per 100 possessions scored and allowed by
the team (their ratings), Var() indicates the variance of the quantity
in parentheses, and Cov() indicates the covariance of
the quantity in parentheses.
For those who are math-phobic, you should just understand that
the larger the term in brackets above, the greater the chance
of winning. So if you increase your points per 100 possessions
rating while
keeping everything else constant, you increase your chance of
winning. That's obvious, right? Well, there are some subtle
ways to increase the above expression. The one I'm thinking
of is when you are an underdog. In this case, you are expected
to win less than 50% of the time. This means that the above
expression in brackets is less than zero; PPG is less than Opp.PPG.
When the top is negative, one way to increase the overall value of
the term in brackets is to increase the bottom. This may not
be very obvious to people without a statistics course or two
(or three or four) in their background, but you can increase
the denominator by slowing down the game.
"Huh?" You say. OK, that last statement was a bit of a leap,
but it is true. You can trust me and jump to the next paragraph
or you can continue reading this one. By slowing down the game,
a team reduces the number of possessions on which it can score.
The variance of the team's rating and the variance of the opposition's
rating both increase with fewer possessions. This is known
from the binomial distribution, which is used to describe
coin flips. This distribution says that the variance of the
probability of success (the probability of scoring
on a possession, or the variance of a team's rating) is
described by
Var(observed probability) = p*(1-p)/n
where p is the "true" probability of scoring
for each team (which gives us the basis for one team being
the underdog, and n is the number of possessions.
If you decrease n, you increase the variance
of the "observed probability", or the probability seen
by a team attempting to score on n possessions.
If you can follow the math, you see how slowing the game
increases the variance of the "observed probability" of
scoring for both the offense and defense (which
translates to a higher variance of offensive and
defensive ratings), which then makes the term in
brackets up above less negative or higher. Hence,
an underdog increases its chances of winning to something
closer to 50%.
In the extreme, this principal is easy to understand. Look
at the Bulls and the 76ers. Over the course of a 95 possession
game, it's an easy pick -- you take the Bulls to win. Now,
consider a game shortened to one minute. The 76ers have a lot
better chance to win, don't they? It's not uncommon for
a losing team to go on a four point "run" over the course of
a minute. But it is uncommon that a bad team like the Sixers
will keep that run going over the course of 95 possessions.
So, if the Sixers could just manage to slow the game so that
only four possessions are used, they just might beat the Bulls...
Of course, this is why basketball instituted a shot clock.
I should follow this scientific explanation up by emphasizing
that there are teams that increase their rating by slowing
the pace or picking up the pace. I believe this, but have
never tried to measure it. This is, of course, important
and can offset the principal I demonstrated above. However,
what I demonstrated above is not trivial, nor is it a strategy
to ignore. It has certainly not been ignored by the
Princeton Tigers of the world.
Tracing the Pace and Efficiency of the NBA
The following plot shows the progress of
points per game, possessions
per game, and
ratings (points per possession)
from the '73-74 NBA
season to last season:
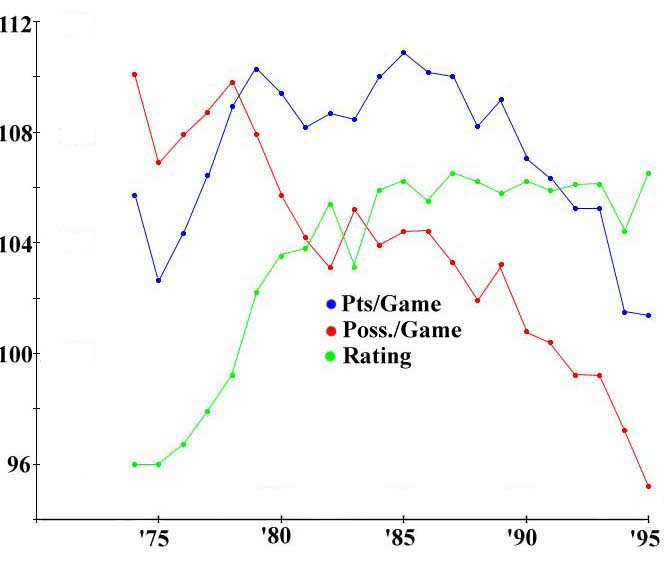
Notice how the pace has gotten dramatically slower, but the efficiency of
the offense has mostly improved, though it's been
pretty level since the mid 1980's. It's always hard to say exactly
why such major changes have occurred in the game. I'm
not sure people were conscious of the pace slowing until the past couple
years. In 1988 or so, Martin Manley, author of
Basketball Heaven, wrote to me suggesting that the
pace was going to increase in the future, this despite the
trend already evident at the time that the pace was slowing.
I'm sure it has slowed even further this season, though I haven't
done the calculations. Statistically, the number of turnovers
and the number of shots have both decreased, while the number
of free throws and offensive rebounds have roughly remained
steady. Basically, teams have begun to take better care of the ball
and shoot better, which is not entirely surprising.
There is one big glitch in the history of scoring efficiency
and that is the big dip in the 1994 season. I cannot recall
any big change in the rules to help the defense that year. In
fact, I believe that was about the time officials began enforcing
brutality in the paint a bit more, increasing their calls again the
following year. Someone correct me if I'm wrong, but
I can only think of one big change in the league that
season -- Michael Jordan didn't play. Sure, he didn't play
much in 1995 either, but they moved the three-point line in
a couple feet, too, and that brought the league's
scoring efficiency back up.
But Jordan couldn't affect the league that much...could he?